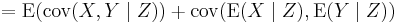Law of total covariance
In probability theory, the law of total covariance[1] or covariance decomposition formula states that if X, Y, and Z are random variables on the same probability space, and the covariance of X and Y is finite, then
The nomenclature in this article's title parallels the phrase law of total variance. Some writers on probability call this the "conditional covariance formula"[2] or use other names.
(The conditional expected values E( X | Z ) and E( Y | Z ) are random variables in their own right, whose values depends on the value of Z. Notice that the conditional expected value of X given the event Z = z is a function of z (this is where adherence to the conventional rigidly case-sensitive notation of probability theory becomes important!). If we write E( X | Z = z) = g(z) then the random variable E( X | Z ) is just g(Z). Similar comments apply to the conditional covariance.)
Contents |
Proof
The law of total covariance can be proved using the law of total expectation: First,
from the definition of covariance. Then we apply the law of total expectation by conditioning on the random variable Z:
Now we rewrite the term inside the first expectation using the definition of covariance:
Since expectation of a sum is the sum of expectations, we can regroup the terms:
Finally, we recognize the final two terms as the covariance of the conditional expectations E[X|Z] and E[Y|Z]:
Notes and references
See also
- Law of total variance, a special case corresponding to X = Y.
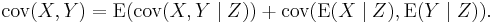
![\operatorname{cov}[X,Y] = \operatorname{E}[XY] - \operatorname{E}[X]\operatorname{E}[Y]](/2012-wikipedia_en_all_nopic_01_2012/I/3d993a59e764b2e7cab395718ba72d20.png)
![= \operatorname{E}[\operatorname{E}[XY\mid Z]] - \operatorname{E}[\operatorname{E}[X\mid Z]]\operatorname{E}[\operatorname{E}[Y\mid Z]]](/2012-wikipedia_en_all_nopic_01_2012/I/fc9f36f2020ceb6fd0d2d64c23e35042.png)
![= \operatorname{E}\!\left[\operatorname{cov}[X,Y\mid Z] %2B \operatorname{E}[X\mid Z]\operatorname{E}[Y\mid Z]\right] - \operatorname{E}[\operatorname{E}[X\mid Z]]\operatorname{E}[\operatorname{E}[Y\mid Z]]](/2012-wikipedia_en_all_nopic_01_2012/I/3f6edaef07cd2f420848c857e6b2ac0a.png)
![= \operatorname{E}\!\left[\operatorname{cov}[X,Y\mid Z]] %2B \operatorname{E}[\operatorname{E}[X\mid Z]\operatorname{E}[Y\mid Z]\right] - \operatorname{E}[\operatorname{E}[X\mid Z]]\operatorname{E}[\operatorname{E}[Y\mid Z]]](/2012-wikipedia_en_all_nopic_01_2012/I/0585cb2033f2635310871cd43eca289e.png)